Come trovare la radice dell'equazione?

Una delle sezioni principali della matematica è una sezione dedicata alla risoluzione di equazioni e alla ricerca della radice delle equazioni.
Prima di trovare la radice dell'equazione, devi prima capire di cosa si tratta.
La radice dell'equazione è il valore dell'ignotovalori nell'equazione denotata da lettere latine (più spesso - x, y, ma potrebbero esserci altre lettere). Questo è stato menzionato nel nostro articolo - Qual è la radice dell'equazione.
Considera come trovare tutte le radici, su diversi tipi di equazioni e esempi specifici.
L'equazione della forma ax + b = 0
Questa è un'equazione lineare con una variabile, dove a e b sono numeri, e x è la radice dell'equazione.
Il numero di radici dell'equazione dipende dai valori di aeb:
- Se a = b = 0, allora l'equazione ha un numero infinito di radici.
- Se a = 0, b non è 0, quindi l'equazione non ha radici.
- Se a non è uguale a 0, troviamo la radice con la formula: x = - (b / a)
esempio:
- 5x + 2 = 0
- a = 5, b = 2
- x = - (2/5)
- x = -0,4
Risposta: la radice dell'equazione è 0.4
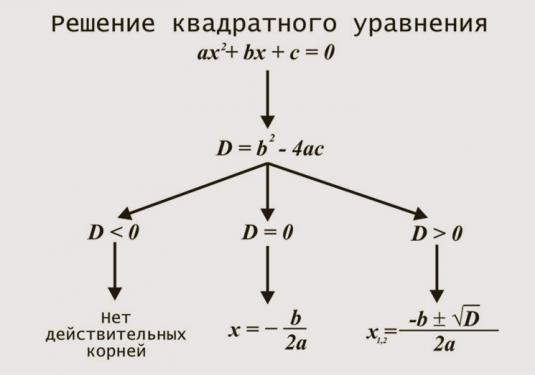
L'equazione è ax2 + bx + c = 0.
Questa è un'equazione quadratica. Ci sono diversi modi per trovare le radici nell'equazione quadratica. Considereremo un generale adatto per la risoluzione di qualsiasi valore di a, b e c.
Innanzitutto, dobbiamo trovare il discriminante (D) di questa equazione.
Per questo, c'è la formula:
- D = b2-4ac
A seconda di ciò che la discriminante ha imparato, ci sono 3 opzioni per ulteriori soluzioni:
- Se D> 0, quindi le radici di 2. E sono calcolate dalle formule:
- x1= (-b + √ D) / 2a.
- x2= (-b - √ D) / 2a
- Se D = 0, allora la radice è una - può essere trovata dalla formula: x = - (b / 2a)
- Se D <0, l'equazione non ha radici.
esempio:
- x2+ 3x-4 = 0
Qui a = 1, b = 3, c = -4
- D = 32 - (4 * 1 * (- 4))
- D = 9- (-16)
- D = 9 + 16
- D = 25
D> 0, quindi ci sono 2 radici nell'equazione.
- √ D = √25 = 5
Sostituiamo tutti i valori nella nostra formula:
- x1 = (-3 + 5) / 2 * 1
- x1= 2/2
- x1= 1
- x2= (-3-5) / 2 * 1
- x2= (-8) / 2
- x2= -4
Risposta: le radici dell'equazione sono 1 e -4.
L'equazione dell'ascia di forma3+ bx2+ cx + d = 0
Questa è un'equazione cubica.
Esistono formule speciali del matematico Cardano, su cui si può risolvere una simile equazione, ma sono molto complesse. Andremo l'altro, in modo più comprensibile.
Le equazioni cubiche ne hanno sempre almeno unaroot, e il suo valore è solitamente un numero intero compreso tra -3 e 3. Cioè, a sua volta sostituiremo l'equazione disponibile per i numeri x: -3, -2, -1, 0, 1, 2 e 3. Questo sarà X1.
È molto più semplice e veloce di quanto sembri, e sicuramente più semplice dell'uso delle formule Cardano.
Dopo troviamo x1 , vai alla ricerca X2 e X3.
A tal fine, dividiamo la nostra equazione in (x-x1) - questo può essere fatto facendo le parentesi. Dobbiamo avere un'equazione quadratica, che abbiamo risolto in questo articolo un po 'più in alto.
esempio:
- x3 - 3 volte2 - 13x + 15 = 0
Con il metodo di selezione scopriamo che X1= 1, cioè, dobbiamo dividere la nostra equazione in (x-1)
Di conseguenza, otteniamo:
- x2 - 2x - 15 = 0
Abbiamo ottenuto un'equazione quadratica. Lo risolviamo come sopra. E arriviamo al fatto che ha 2 radici: - 3 e 5.
rispondere:
- Le radici dell'equazione: x1= 1, x2= -3, x3 = 5.
Maggiori informazioni possono essere trovate nell'articolo Come risolvere le radici.