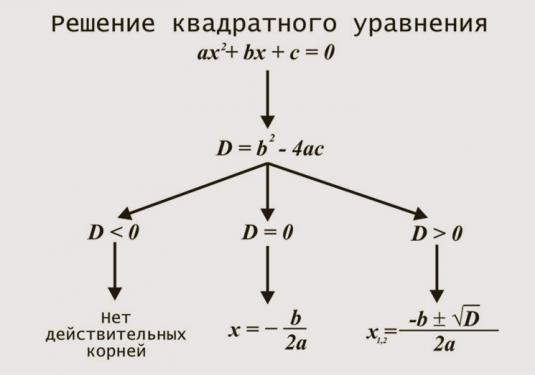
Come risolvere le equazioni per la classe 5?

Un'equazione è un'equazione in cui esiste un termine sconosciuto - x. Il suo significato deve essere trovato.

Una quantità sconosciuta è chiamata la radice dell'equazione. Risolvere l'equazione significa trovare la sua radice, e per questo è necessario conoscere le proprietà delle equazioni. Le equazioni per la classe 5 sono semplici, ma se impari a risolverli correttamente, non avrai problemi con loro in futuro.

La proprietà principale delle equazioni

Quando entrambi i lati dell'equazione cambiano della stessa quantità, continua ad essere la stessa equazione con la stessa radice. Risolviamo alcuni esempi per capire meglio questa regola.

Come risolvere le equazioni: aggiungere o sottrarre

Supponiamo di avere un'equazione della forma:

a + x = b - qui a e b sono numeri, e x è un termine sconosciuto dell'equazione.

Se aggiungiamo (o sottraiamo) le quantità c a entrambi i lati dell'equazione, non cambierà:

a + x + c = b + c
a + x - c = b - c.

Esempio 1

Usiamo questa proprietà per risolvere l'equazione:

37 + x = 51

Sottrarre il numero 37 da entrambe le parti:

37 + x-37 = 51-37

otteniamo:

x = 51-37.

La radice dell'equazione è x = 14.

Se osserviamo attentamente l'ultima equazione, vedremo che è uguale alla prima. Abbiamo semplicemente trasferito il termine 37 da una parte all'equazione, sostituendo il segno più per meno.

Si scopre che qualsiasi numero può essere trasferito da una parte dell'equazione a un'altra con il segno opposto.

Esempio 2

37 + x = 37 + 22

Eseguiamo la stessa azione, trasferiamo il numero 37 dal lato sinistro dell'equazione a destra:

x = 37-37 + 22

Dal 37-37 = 0, quindi lo accorciamo semplicemente e otteniamo:

x = 22.

Gli stessi termini dell'equazione con un segno, che sono in diverse parti dell'equazione, possono essere abbreviati (omessi).

Moltiplicazione e divisione delle equazioni

Entrambe le parti dell'equazione possono anche essere moltiplicate o divise per lo stesso numero:

Se l'uguaglianza a = b è divisa o moltiplicata per c, non cambierà:

a / c = b / c,
ac = bc.

Esempio 3

5x = 20

Dividiamo entrambi i lati dell'equazione per 5:

5x / 5 = 20/5.

Dal 5/5 = 1, quindi riduciamo questo fattore e il divisore nella parte sinistra dell'equazione e otteniamo:

x = 20/5, x = 4

Esempio 4

5x = 5a

Se entrambi i lati dell'equazione sono divisi per 5, otteniamo:

5x / 5 = 5a / 5.

5 nel numeratore e nel denominatore del lato sinistro e destro sono abbreviati, otteniamo x = a. Quindi, gli stessi fattori nei lati sinistro e destro delle equazioni sono ridotti.

Risolviamo un altro esempio: