Come trovare il seno di un angolo acuto di un trapezio?

Il trapezio è un quadrilatero con due lati paralleli tra loro. Considera come trovare il seno di un angolo acuto di un trapezio usando come esempio il trapezio ABCD, in cui i lati AD e BC sono paralleli.

Stiamo cercando il seno dell'angolo di un trapezio isoscele

Considera un trapezio isoscele. In un trapezio isoscele, i lati sono uguali. Nel nostro caso, AB = CD = 25, e la dimensione delle basi è AD = 65 e BC = 51. Proviamo a trovare il seno dell'angolo acuto.

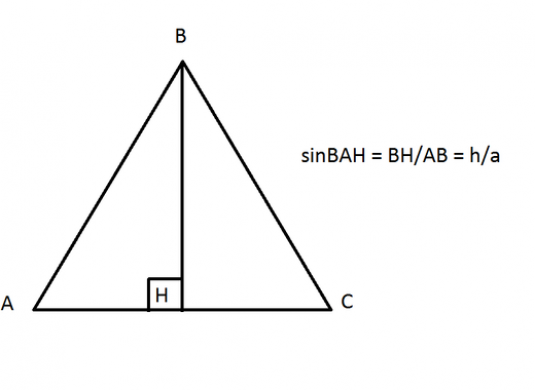
Come sapete, il seno è uguale al rapporto tra la gamba opposta e l'ipotenusa, quindi abbiamo bisogno di un triangolo rettangolo. Lo otteniamo facendo cadere il BH perpendicolare dall'angolo ABC alla base.

Una caratteristica importante dei trapezi è la loroaltezza - la distanza tra lati paralleli, che di solito sono chiamati base. Per determinare questa distanza, è necessario abbassare la perpendicolare all'altra base dall'angolo della base più piccola (solitamente superiore). Nel nostro caso, queste saranno le perpendicolari di VN e CE, che abbiamo bisogno di determinare il seno.

Determinare l'altezza del trapezio

Otteniamo due triangoli rettangolari, con le gambe BH = CE e l'ipotenusa AB = CD. Di conseguenza, le altre gambe di questi triangoli sono uguali a AH = ED.

Poiché nel quadrilatero HBSE tutti gli angoli sono diritti (HB e CE sono perpendicolari alle basi), quindi abbiamo ricevuto un rettangolo con i lati BC = CE.

AD = AH + HE + ED per costruzione. Poiché AH = ED e HE = BC, questa equazione può essere scritta come: